삼각법(trigonometrics) 삼각비중학교 레벨삼각함수와 역수고등학교 레벨삼각함수의 미적분고등학교 레벨삼각함수의 역함수와 미분고등학교~대학 레벨쌍곡선함수의 역함수와 미분대학교 레벨 2019년 10월(정확히 3년 전) 블로그에 글을 대충 쓰던 시절 수학에서의 삼각비(trigonometric ratio)를 처음 배우는 이들을 위한 글을 쓴 적이 있었습니다. 지금까지 4만2,000여명이 방문하셔서 여전히 제 블로그 인기글 상위권을 차지하고 있지만 아쉽게도 글의 퀄리티에 별로 신경을 쓰지 않던 시절이라 글이 굉장히 난잡했습니다. 오늘 한번 그때의 느낌을 살려서 더 예쁘고 직관적으로 다시 쓰려고 합니다.
세부사항은이쯤에서…예전에중학교수학선생님이좋아했던표현을조금사용해서삼각비가뭔지살펴보도록하겠습니다.
삼각비(3개)
피타고라스 아저씨가 세상의 도리를 깨우치려고 하기 훨씬 전에 태초에 이런 직각삼각형이 하나 있었어요.
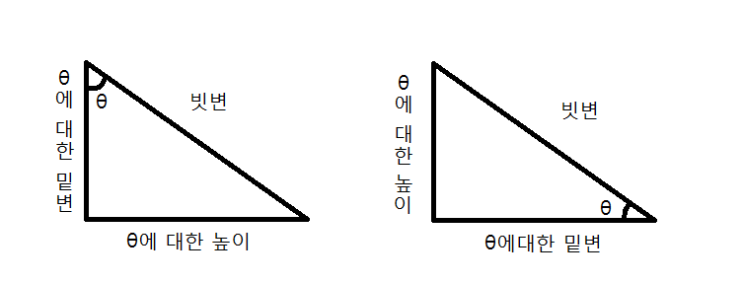
둔각삼각형은요? 예각삼각형은안돼요? 안 돼요. 삼각비랑 나중에 배울지도 모르는 삼각함수는 직각삼각형을 너무 좋아해서요. 우선 정의는 직각삼각형이라고 가정하기 때문이죠.

삼각비를 배우는 친구 중 순수한 친구 때문에 마음이 아픈 부분은 조금 브러 처리를 해봤습니다.
삼각비(trigonometric ratio). 한자나 영어에 약간 센스가 있으신 분들은 아시겠지만 삼각형이 있는 부분에 대한 비율(ratio)입니다. 여기서 어떤 부분은 삼각형의 각 변(side)의 길이 비율이에요. 이제 삼각비의 정의를 살펴보겠습니다.직각삼각형의 3변 길이 중 2변 길이 간의 비례관계를 나타내는 값이다.삼각비
중학교 때 처음 배우는 삼각비는 총 3가지가 있는데, 그 후에 고등학교에서 미적분을 배울 경우 3가지를 더 배우게 되는데, 여기서는 이 6가지를 정리해서 다루도록 하겠습니다. 어렵지 않아요! 일단 기본적인 세 가지부터 알아볼게요. 아까 태초에 탄생한 아름다운 직각 삼각형을 다시 꺼내봤습니다. 삼각형의 세 변을 각각 아래 그림과 같이 a, b, c라고 합니다.
그럼 각 B(그리기 부분)에 대한 기본적인 삼각비 3가지는 다음과 같습니다. 위에서 정의된 대로 직각삼각형의 2각의 비임을 단번에 알 수 있습니다. sin은 사인(sine), cos는 코사인(cosine), tan은 탄젠트(tangent)로 각각 읽습니다.이를 일반화하여 나타내면 다음과 같습니다. 아까 그 아름다운 직각삼각형의 그림을 보세요.다만 외우기에는 다소 무리가 있을 수 있지만 아래와 같이 아름다운 직각삼각형에 각각 삼각함수 기호 sin, cos, tan을 필기체처럼 써보시면 금방 외우실 수 있을 것 같습니다.

참고로 이미 아시는 분들도 계시겠지만 tan(탠젠트)은 sin(사인)과 cos(코사인)만을 사용해서 나타낼 수 있습니다. 이유는 위의 아름다운 직각 삼각형을 이용하여 쉽게 파악할 수 있습니다. 여기서는 sinB와 cosB를 통해 tanB를 나타냅니다. 그 밖에 더 중요한 성질은 삼각함수 파트에서 배우는데 아래 내용도 유용하게 많이 쓰이기 때문에 어차피 삼각비를 배운 것을 하나 더 배워가시기 바랍니다.여기까지가 기본 삼각비 3가지입니다.삼각비(3개+3개)
삼각비는 3개가 아니라 6개라는 것을 말씀드린 적이 있습니다. 각각 아까 말씀드린 sin(사인), cos(코사인), tan(탠젠트)의 역수인데, 이 6개의 삼각비를 사용하면 직각삼각형의 모든 2변 길이의 비율을 나타낼 수 있습니다. 삼각비를 처음 배워봐서 부담스러우신 분들은 패스하셔도 됩니다.

어차피 <미적분>을 공부하는 친구들은 적어도 고등학교 과정 때 다시 만나기로 되어 있어요. 그때는 꼭 다시 만나요~ 아래 세 삼각비의 역수는 각각 아래와 같고, csc는 고시콘트(cosecant), sec은 시콘트(secant), cot은 코탄젠트(cotangent)로 읽습니다. csc는 sin의 역수, sec은 cos의 역수, cot은 tan의 역수임을 알아두세요. 특히 cot은 tan의 역수입니다. 여담입니다만, 이전에 조사한 tan=sin/cos를 뒤집어 cot=cos/sin인 것까지 기억하시면 더 좋을 것 같습니다. 처음에는 외우는 것으로 조금 힘들지만 단순한 역수 관계이기 때문에 금방 익숙해질 거라고 생각합니다.저는 개인적으로 sin-csc/cos-sec/tan-cot으로 해서 더 쉽게 외웠습니다. 서로 반대라서 글자도 반대.어때요?
한편…왜 굳이 1/sin이라고 쓰지 않고 외우는 것이 더 많아지도록 csc(코시 콩트)라는 기호를 만들어 사용하는 걸까요? 물론 개인적인 생각이긴 하지만… 저도 중학교 때는 잘 몰랐습니다. 그런데 시간이 지나면서 나이가 들면서 미적분을 공부하고 여러 가지 복잡한 식 중에서 저런 삼각형을 다루는 일은 점점 많아지고… 이 때마다 저렇게 분수로 쓰면 식이 복잡해지고 헷갈리기 때문에 오히려 세 가지를 기호로 지정하여 외우는 한이 있더라도 그렇게 하는 것이 편하기 때문임을 스스로 깨달았습니다.
그리고 수학자는 가능한 간결하고 쓰기 위해 어떻게든 노력하는 사람들이기 때문이라는 것을 잊지 마세요. 마치 영어로 ‘Iam’을 굳이 ‘I’m’으로 줄여서 쓰는 것과 다르지 않습니다. 삼각함수의역함수를외우는이유는충분히알수있었기때문에여러번반복학습하면서암기하는것만남았습니다.

자, 외웁시다. 사인의 역수는 고시콘트. 코사인의 역수는 씨콘트. 탄젠트의 역수는 코탄젠트. 기억할 수 있다. 기억할 수 있다. 영원히. 특수삼각비의 각
삼각비에 익숙해지면 아래의 특수한 직각 삼각형 두 가지를 마주해야 합니다. 이번뿐만 아니라 앞으로도 만날 존재이니까 서로 웃는 얼굴로 마주해요. 첫 번째는 직각, 나머지 두 모서리는 각각 45도의 직각 삼각형입니다.
놀랍게도 이것의 각 변의 길이 비율은 정확히 1:1:Φ2로 두 개의 특이한 직각 삼각형 중 하나로 꼽힙니다.

두 번째로 특이한 놈은 1각이 30도, 1각이 60도, 1각은 직각의 직각삼각형이고 각 변의 길이는 정확히 아래 그림과 같이 1:Φ3:2의 비율을 가지고 있습니다. 따라서 각이 60도인 곳을 ᅡᄀ라고 하면 sin, cos, tanᄋ의 값은 다음과 같습니다. 그러면 나머지 저 한 변… 다시 말해 30도인 곳은 삼각비가 어떻게 되는 걸까요? 삼각형을 돌리고 나서 다시 삼각비를 보면 되기 때문에 그렇게까지 그림을 첨부할 수는 없지만 어렵지 않게 찾을 수 있을 겁니다. 답은 바로 아래 표에 정리되어 있습니다.

이렇게 삼각비 값을 0도, 30도, 45도, 60도, 90도씩 정리해서 표로 정리해 보면 다음과 같습니다. 물론 삼각형을 저렇게 처음에는 그려서 값을 유추하겠지만 워낙 자주 나오니까 빨리 익숙해져서 머리에서 삼각형을 만들어서 순식간에 대응하는 삼각비 값을 바로 낼 수 있어야 합니다.
일단 sin, cos, tan에만 익숙해지면 그에 대한 역수인 csc, sec, cot은 나중에 저절로 머리에 들어올 것입니다. 뒤집기만 하면 돼요. 저도 경험해봤는데 처음부터 이걸 한 방에 다 외우라는 건 무리인 것 같아요. 그러니까 서두르지 말고 처음에는 직각 삼각형을 먼저 선으로 저어주거나 하면서 삼각비와 아래 표에 대한 내용에 서서히 익숙해 지시기 바랍니다. (아니면… 고등학교 과정에서 <미적분>을 볼 때 다시 공부하셔도 됩니다.웃음) 삼각비 특수 각표 각도 0°30°45°60°90° sin 01/21/Φ2Φ3/21 cos1Φ3/21/Φ21/20tan 01/Φ31Φ311/Φ30ccΦ2Φ22/Φ31sec12/Φ3Φ22*중학교 때는 개인적으로 정말 수학이 어렵고 싫었습니다. 그 표를 처음 봤을 때 제가 얼마나 울고 싶었는지 누가 알았으면 좋겠다고 생각할 정도였습니다. 결국 남들보다 시간은 오래 걸렸지만 지금은 삼각비, 삼각함수 등과 친하게 지내고 있습니다.삼각비 사용법
마지막으로 삼각비. 게다가 이제 수학을 공부한다면 삼각함수와 그 뒤의 내용이 왜 쓰이는지 간단하게 살펴보겠습니다. 물론 학교 시험에 나와서 공부한다는 것도 하나의 현실적으로 슬픈 이유이기도 하지만, 저는 개인적으로 그런 목적으로만 수학을 공부하는 것을 좋아하지 않고 대신 꼭 어떻게 응용할 수 있는지를 확인하는 것을 좋아합니다.
삼각비가 사용되는 대표적인 예가 삼각법입니다. 아래 그림을 볼까요? 제가 간단하게 산 꼭대기에 정체불명의 아주 작은 야자수(?)가 펼쳐진 작은 인공산을 태블릿 펜으로 하나 만들었어요. 저기 밑에 제가 있을게요. 저는 이 산의 높이를 측정하고 싶습니다.
태블릿으로 간단하게 그려봤어요. 비율이 이상한 점은 양해 부탁드립니다.이때 산을 직접 잘라 단면의 높이를 측정하지 않고도 산의 높이를 측정할 수 있습니다. 먼저 산의 각도를 재봅시다. 대략 45도네요.
일단 야자수를 습격해서 야자수를 하나 따먹을 겸 산까지 경사를 타고 올라왔고 거리를 계산해보니 대략 30m인 것을 확인할 수 있었습니다. 이것으로 인공산의 높이를 알 수 있습니까? 네, 가능합니다.
벌써 야자수만한 야자수를 따갔군요. 비율이 이상한 세상인 것 같아요.이전 단계에서 우리는 어느새 한쪽이 45명의 직각이 등변 삼각형을 만들고 있었다는 것을 깨달았습니까? 그럼 아까 배운 것을 이용해서 바로 높이를 구해보도록 하겠습니다. 높이는 대략 21.213m로 우리는 인공산을 직접 자르지 않고도 인공산의 높이를 삼각비를 사용하여 구했습니다.
실제로 이렇게 삼각법을 활용하는 부분은 학교 시험에도 물론 건축 현장이나 지도 제작, 천문학 등 현업에도 널리 쓰이는 방식입니다. 수학의 힘을 활용하여 단순히 높이 21m의 인공산의 높이를 재는 것뿐만 아니라 물체가 서로 멀어지는 속도나 지구와 태양의 거리처럼 매우 긴 거리를 구할 때도 삼각법을 응용하여 구할 수 있습니다. 대단하죠?부디 저의 소박한 예가 삼각비 활용에 대한 이해에 도움이 되었으면 합니다.이상 삼각함수가 무엇이고 어떻게 정의되는지, 그리고 수상한 작은 야자수가 자란 작은 인공산의 높이를 구해보는 예를 통해서 간단하게 삼각비를 응용도 해보았습니다. 저의 이 글이 삼각비와 삼각함수, 나아가 미적분을 장차 공부하려는 모든 분들에게 작지만 소소한 초석이 되었으면 합니다. 오랜만에 저도 지금은 고3이긴 하지만 중1 때 처음 삼각우를 보면서 당황했던 기억을 떠올리며 최대한 쉽게 쓰기 위해 노력했는데 다른 분들께 잘 전달됐는지 모르겠네요.
그런데 어쨌든 개인적으로 이 삼각비를 충실히 이해하고 잘 공부해서 충분히 얘들과 친해진다면 앞으로 수학 공부는 훨씬 재미있고 쉬울 거라고 장담할 수 있습니다. 앞으로 볼 내용이 많으니까요.(유감스럽게도 저는 그 반대로 경험을 했습니다. 그래서 여러분은 저와 같은 경험이 없기를 바랍니다.삼각법(trigonometrics) 삼각비중학교 레벨 삼각함수와 역수고등학교 레벨 삼각함수의 미적분고등학교 레벨 삼각함수의 역함수와 미분고등학교~대학 레벨 쌍곡선함수와 미분대학교 레벨 쌍곡선함수의 역함수와 미분대학교 레벨*꾸준히 연재해 보아야 합니다.
파워포인트로 중간에 제가 그림을 그린 내용은 아래에 있습니다. 필요하신 분들은 사용하세요!
글에 틀린 내용, 개선하고 싶은 내용이 있으면 주체 없이 알려주세요. 여러분의 지적이 더 나은 글을 만들고, 저는 언제든지 기꺼이 그런 비판을 받아들이려는 의지가 충만합니다.